| Version 28 (modified by , 9 years ago) (diff) |
|---|
Project Name
| Infrastructure | CNRS_Coriolis |
| Project (long title) | Coriolis and Rotational effects on Stratified Turbulence |
| Campaign Title (name data folder) | 16CREST |
| Lead Author | Jeffrey Peakall |
| Contributor | Stephen Darby, Robert Michael Dorrell, Shahrzad Davarpanah Jazi, Gareth Mark Keevil, Jeffrey Peakall, Anna Wåhlin, Mathew Graeme Wells, Joel Sommeria, Samuel Viboud |
| Date Campaign Start | 12/09/2016 |
| Date Campaign End | 21/10/2016 |
1 - Objectives
Our primary objective is to measure detailed turbulence distributions within channelised gravity currents, as a function of Coriolis forces, concentrating on: i) the bottom boundary layer, ii) redistribution of turbulence within bends, and, iii) redistribution of turbulence at the interface between the gravity current and the ambient. These datasets will enable existing theory on the presence and influence of Ekman boundary layers to be tested, with important implication for the basal shear stress distributions, erosion, and the evolution of channels. These data on the distribution of turbulence will then be applied to i) examine the turbulence distribution in straight channels, ii) provide an analysis of secondary flow and associated turbulence around bends for the first time, and an assessment of how channelized flows alter as a function of Rossby numbers and therefore latitude, iii) assess how the morphodynamics of submarine channels vary as a function of the Rossby number, iv) explain the observed patterns of submarine channel sinuosity with latitude (Peakall et al., 2012; Cossu and Wells, 2013; Cossu et al., 2015), and, v) incorporate the entrainment data into numerical models of submarine channels, in order to address the unanswered question of how these flows traverse such large-distances across very low-angle slopes (Dorrell et al., 2014).Our primary objective is to measure detailed turbulence distributions within channelised gravity currents, as a function of Coriolis forces, concentrating on: i) the bottom boundary layer, ii) redistribution of turbulence within bends, and, iii) redistribution of turbulence at the interface between the gravity current and the ambient. These datasets will enable existing theory on the presence and influence of Ekman boundary layers to be tested, with important implication for the basal shear stress distributions, erosion, and the evolution of channels. These data on the distribution of turbulence will then be applied to i) examine the turbulence distribution in straight channels, ii) provide an analysis of secondary flow and associated turbulence around bends for the first time, and an assessment of how channelized flows alter as a function of Rossby numbers and therefore latitude, iii) assess how the morphodynamics of submarine channels vary as a function of the Rossby number, iv) explain the observed patterns of submarine channel sinuosity with latitude (Peakall et al., 2012; Cossu and Wells, 2013; Cossu et al., 2015), and, v) incorporate the entrainment data into numerical models of submarine channels, in order to address the unanswered question of how these flows traverse such large-distances across very low-angle slopes (Dorrell et al., 2014).
2 - Experimental setup:
2.1 General description
| Run Name | Measurement Position | Density Excess | Input flow | Rotation Rate | Initial Water Depth | Outflow Rate | Run Time | ADV Dwell Time |
| $(kg\m3)$ | $(ls-1)$ | $(rad\s-1)$ | $(m)$ | $(ls-1)$ | $(Minutes)$ | $(s)$ | ||
| Smooth_1 | 1 | 20 | 12 | 0 | 1 | 5.5 | 20 | 60 |
| Smooth_2 | 1 | 20 | 12 | 0 | 1 | 12.0 | 20 | 60 |
| Smooth_3 | 2 | 20 | 12 | 0 | 1 | 5.5 | 20 | 60 |
| Smooth_4 | 3 | 20 | 12 | 0 | 1 | 5.5 | 20 | 60 |
| Smooth_5 | 4 | 20 | 12 | 0 | 1 | 5.5 | 20 | 60 |
| Smooth_6 | 1 | 20 | 12 | 0 | 1 | 5.5 | 20 | 30 |
| Smooth_7 | 3 | 20 | 12 | 0 | 1 | 5.5 | 20 | 30 |
| Smooth_8 | 4 | 20 | 12 | 0 | 1 | 5.5 | 20 | 30 |
| Smooth_9 | 2 | 20 | 12 | 0 | 1 | 12.0 | 60 | 30 |
2.3 General description
| Notation | Definition | Valve | Remarks |
| $Q_0$ | Input Density | $12 \ (ls-1)$ | |
| $\Delta\rho$ | Density Difference | $20 \ (kg\m3)$ | |
| $W$ | Channel Width | $0.6 \ m$ | |
| $\nu$ | Viscosity | $10-6m2s-1$ |
2.4 Definition of the relevant non-dimensional numbers
Flow Reynolds number across the obstruction, $Re = Uh/\nu$.
Internal composite Froude number across the obstruction, $Fr = U/(g'h){1/2}$, $g' = g(\Delta\rho)/\rho_0$.
Rossby number, $Ro = U/fW$.
Attachments (5)
-
section 500x600 lg 11010.PDF (195.7 KB) - added by 9 years ago.
Drawing Model on Table
-
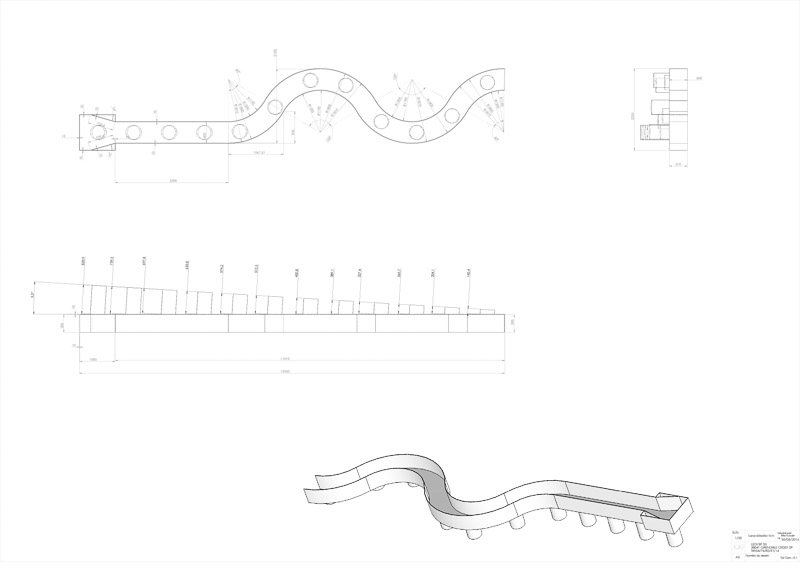
Set_up_drawing.png (212.8 KB) - added by 9 years ago.
Drawing
- Set_up_drawing.jpg (53.9 KB) - added by 9 years ago.
-
Traverse.pdf (46.1 KB) - added by 9 years ago.
Traverse set up for main experiments
-
CRESTTraverseMeasurement.jpg (340.5 KB) - added by 9 years ago.
CREST Traverse Measurement - main experiments
Download all attachments as: .zip